Horizon de placement & rendement composé

Dans cet article, tu vas en apprendre plus sur le rendement composé et découvrir deux calculs qui expliquent pourquoi Selma se concentre sur l'investissement à long terme. L'effet que le rendement composé peut avoir sur ton argent si tu investis assez longtemps relève presque de la magie.

La magie du rendement composé

Il existe un concept financier qui semble extrêmement ennuyeux, mais qui ressemble en fait à un véritable tour de magie qui se révèle avec le temps : les intérêts composés – et par extension, le rendement composé.

Le rendement composé produit un maximum d'effet sur la croissance de ton argent lorsque tu investis aussi tôt et aussi longtemps que possible. On parle ici de plusieurs années : de préférence 10, 15 ou même plus.

La magie réside dans un concept simple. Si tu gardes ton argent assez longtemps sur un compte de placement (utilisant la bonne stratégie et bien entretenu), petit à petit, tes intérêts commencent à générer eux-mêmes des intérêts, sans te demander beaucoup d'efforts.

Comment fonctionne le rendement composé ?

« Le rendement composé (aussi appelé « intérêts composés ») correspond aux intérêts calculés sur le capital initial et qui comprennent tous les intérêts accumulés des périodes antérieures d'un dépôt ou d'un prêt. »
– Investopedia (traduit de l'anglais), 2022

D'accord. Maintenant, expliquons ça en langage clair. 😅 Un exemple est toujours plus parlant. Pour simplifier la démonstration, tous les exemples ci-dessous ont un rendement annuel moyen de 6 %. Le rendement composé est fictivement généré chaque année en fin d'année, et ne comporte aucun frais.

Imagine que ton premier investissement (ou ton « capital initial », en langage financier plus fantaisiste) soit de 10'000 CHF.

Avec ce rendement annuel moyen de 6 %, tes placements généreraient 600 CHF la première année. Après un an, tu aurais donc 10'600 CHF au total.

Facile. Et ensuite ?

La deuxième année, avec le même rendement fictif de 6 %, tu aurais 11'200 CHF. C'est bien ça ?

👩🏻‍🔬 Presque. C'est là que les choses deviennent intéressantes. En raison des « intérêts sur les intérêts », tu obtiendrais 36 CHF supplémentaires ! Ils représentent le retour sur investissement que tu obtiendrais après la première année : 6 % de 10'600 CHF = 636 CHF.

À la fin de la deuxième année, tu aurais donc déjà 11'236 CHF.

C'est fou ce que dix ans passent vite ! Et avec le même rendement solide qui nous sert d'exemple, tu devrais t'attendre à avoir 16'000 CHF, n'est-ce pas ?

Ce serait sans compter sur l'effet des intérêts composés ! Les intérêts sur les intérêts auraient continué de s'accumuler, et tu te retrouverais maintenant avec 1'908 CHF de plus.

Après 10 ans, tu aurais donc 17'908 CHF, et non 16'000 CHF. Comme par magie ! 🔮

Le rendement composé calculé au fil du temps

Maintenant que nous connaissons le principe du rendement composé, examinons de plus près les effets du temps sur la magie des intérêts composés. Nora et Harold, nos deux ami·e·s imaginaires, vont nous aider à y voir plus clair.

Investir pendant 40 ans

Nora commence à épargner pour sa retraite. Ou plutôt « pour l'avenir », comme elle dit, car les jeunes adultes ne sont pas tout près de prendre leur retraite. Enfin, mis à part les footballeurs, mais on s'écarte un peu du sujet.

Revenons à notre chère Nora. Voici son profil :

🎂 Âge : 25 ans

⛱ Retraite : dans 40 ans, à 65 ans

🎢 Épargne : 200 CHF/mois

Dans un monde fictif parfaitement stable, quarante ans d'épargne continue et disciplinée rapporteraient 96'000 CHF à Nora. Pas mal, mais qu'en est-il du rendement composé ?

Conservons le même exemple utilisé plus haut.

• Rendement fictif moyen de 6 % par an
• Aucuns frais ou coûts
• Intérêts composés versés annuellement…
• … et calculés sur la somme moyenne de l'année

Le dernier point signifie que le rendement composé est basé sur le montant que Nora détient sur son compte à la fin de l'année, divisé par 12, le nombre de mois dans l'année.

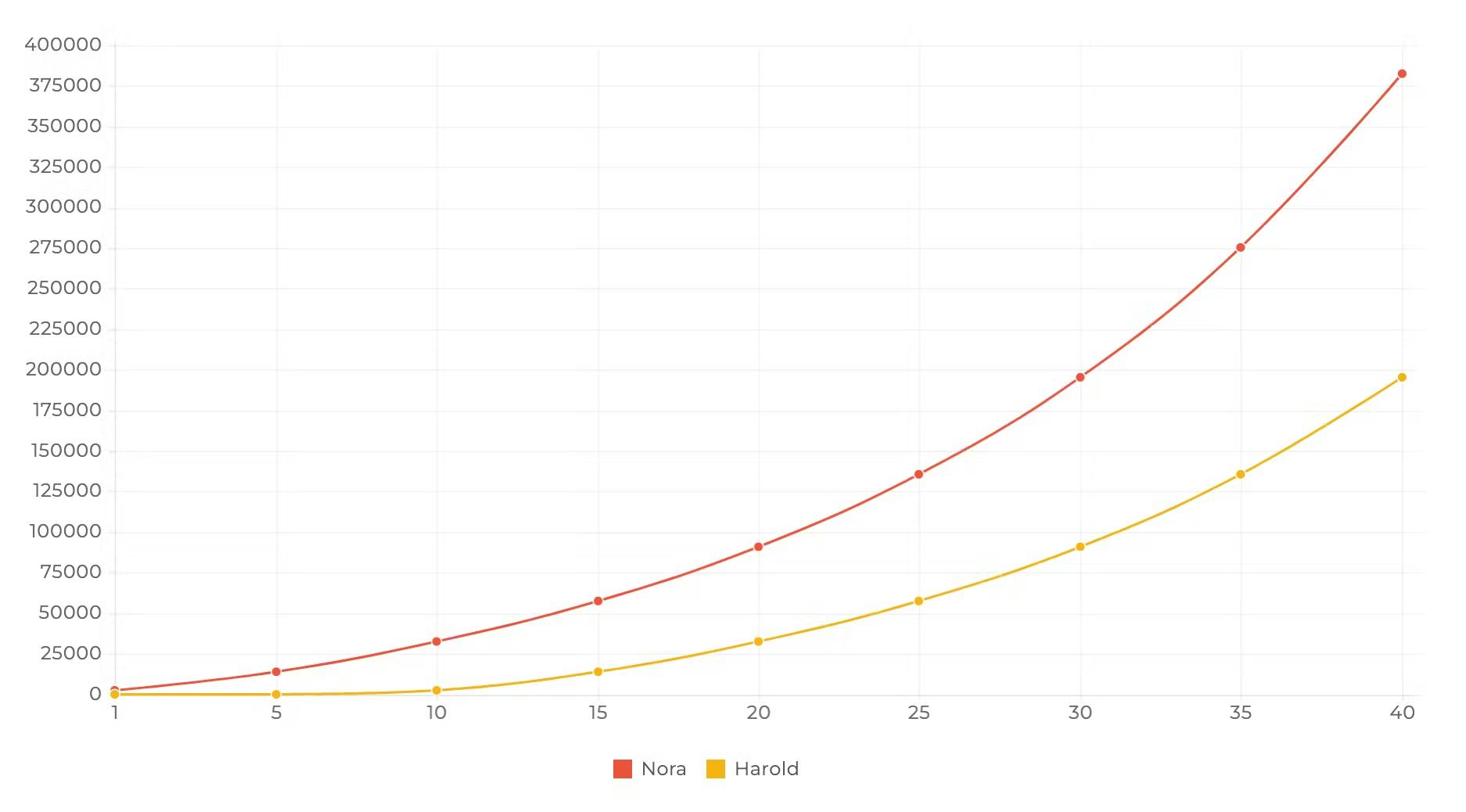
Voici l'épargne de Nora illustrée dans un graphique financier classique. Tu as sûrement déjà vu ce type de graphiques par le passé. Lorsque j'ai regardé celui-ci, je me suis vraiment demandé si j'avais bien lu les chiffres. 🤓

Examinons les chiffres de ce graphique plus en détail. Après quarante années d'épargne ininterrompues, les intérêts composés de Nora, notre rigoureuse épargnante, s'éléveraient à eux seuls à 289'600 CHF ! C'est trois fois plus que ce qu'elle aurait obtenu en déposant simplement son épargne sur son compte bancaire. Merci le rendement composé. 😏

Nora se retrouverait ainsi avec une belle épargne de 382'600 CHF au total. 🔮👩🏻‍🔬

Investir pendant 30 ans

Voilà notre autre ami imaginaire, Harold. À cause de la multitude de publicités de plans d'épargne ciblées et censées être réconfortantes (qui mettent principalement en scène de beaux couples de personnes âgées riant en plein milieu d'un paysage pittoresque), Harold ne peut pas s'empêcher de penser à l'inévitable fuite du temps. Chouette. 🙂

Jusqu'à ce qu'un jour, après des années de petits boulots, Harold décroche un contrat stable. L'image d'un couple de seniors souriants (tirée d'une publicité de plan d'épargne) restée dans un coin de sa tête, il décide finalement de se construire une épargne en investissant.

Le profil d'Harold :

🎂 Âge : 35 ans

⛱ Retraite : dans 30 ans, à 65 ans

🎢 Épargne : 200 CHF/mois

Le graphique précédent donne déjà une idée de ce qui se passerait si les mêmes conditions s'appliquaient.

Après 30 ans d'épargne mensuelle stable, les économies d'Harold s'élèveraient à 72'000 CHF. Les intérêts sur les intérêts ajouteraient environ 123'400 CHF de plus à son épargne. Cela équivaut à près de 195'400 CHF au total. Pas mal ! 🔮👩🏻‍🔬

Même si les investissements mensuels stables de Nora et Harold seraient très fructueux dans les deux cas, l'écart qu'entraîneraient les dix années d'investissement en plus de Nora est assez époustouflant. Avec près de 400'000 CHF, Nora se retrouverait pratiquement avec deux fois plus d'économies qu'Harold.

Cette observation continue de me surprendre et de m'interroger lorsque j'étudie le graphique. Pas toi ? C'est là qu'on se rend vraiment compte que le rendement composé fait des merveilles.

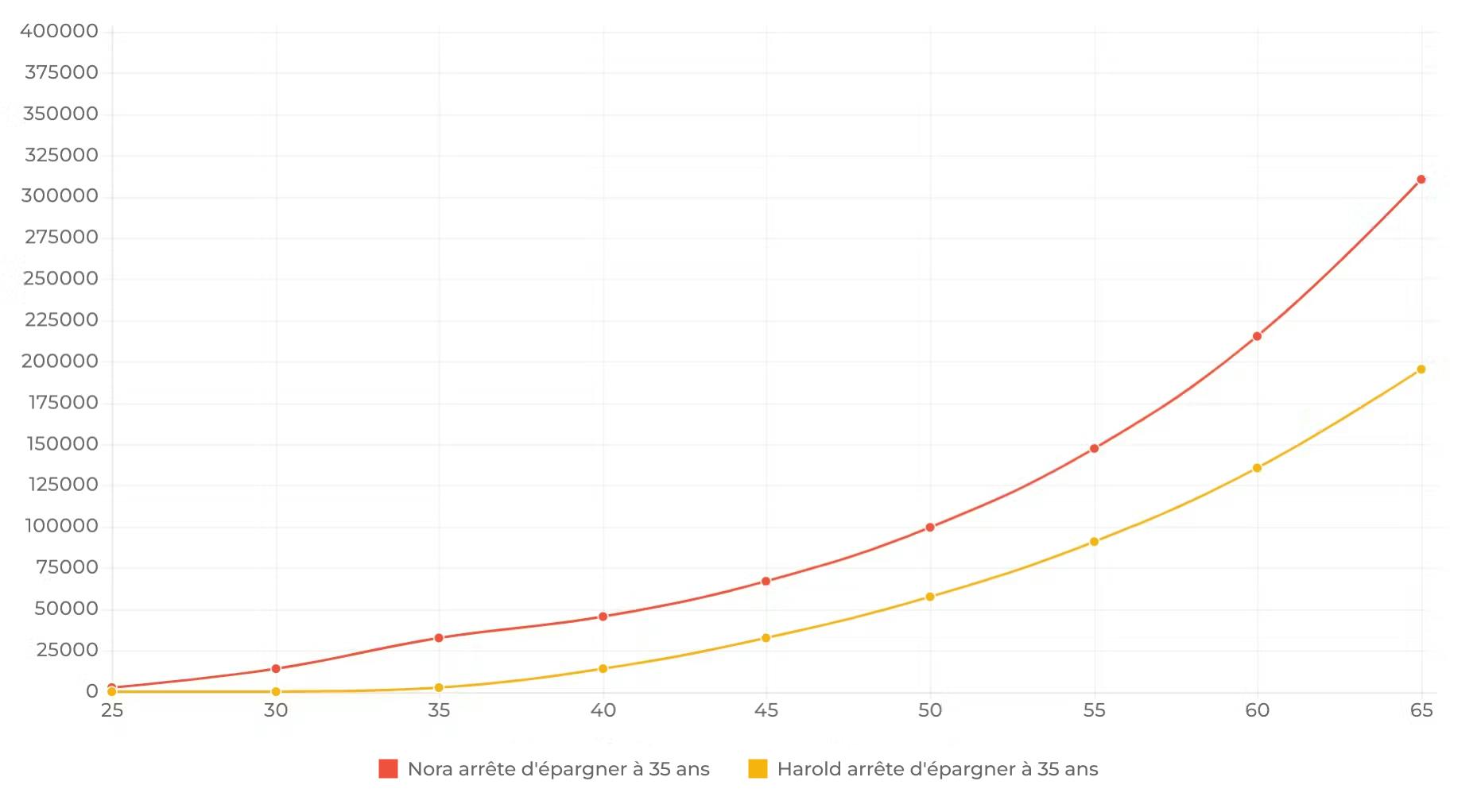
🤓 Imaginons maintenant qu'au bout de dix ans, Nora cesse d'épargner mensuellement. Quelle serait sa performance par rapport à celle d'Harold, qui ne cesserait pas d'investir ? Les investissements d'Harold dépasseraient sûrement ceux de Nora, non ?

🧐 Étonnamment, même si Nora cessait d'investir à 35 ans, l'âge auquel Harold commencerait à investir, la performance de ses investissements resterait bien supérieure à celle des investissements d'Harold.

Nora aurait investi 24'000 CHF au total, contre 60'000 CHF pour Harold. Voilà le résultat lorsque l'on prend en compte le facteur temps (40 ans, dans ce cas !).

Petit conseil si tu doutes après une courte période de temps :

Le secret consiste à s'en tenir au plan. Au bout de cinq ans, le rendement composé semble imperceptible, pas vrai ?

On dirait presque qu'il n'a aucun effet. C'est pourquoi j'ai comparé le rendement composé à un « tour de magie qui se révèle avec le temps ». Il existe bel et bien, mais opère dans l'ombre pendant quelques années. Après dix ou vingt ans, l'écart entre ce que tu avais initialement investi et tes gains générés par les intérêts composés est sidérant.